Activité proposée par : Frédéric JOURDIN et Bernard JOUANNETAUD
Etablissement : Lycée Jean ZAY
2 rue Ferdinand Buisson
45000 Orléans
Thème : Simulation de désintégrations radioactives d’un échantillon de noyaux. Caractère aléatoire d’une désintégration. Approche de la loi de décroissance.
(B.O : Partie B-Transformations nucléaires. 1 Décroissance radioactive)
Classe : Terminale S
Horaires : 2 h
Conditions matérielles :
• Disposer d’une salle informatique avec 1 ordinateur pour deux élèves,
• Logiciel utilisé : EXCEL configuré pour les références circulaires :
« Outils Options Calcul Mode de calcul : Sur ordre ; Cocher la case Itération ; Mettre le nombre maximum d'itérations à 1 »,
• Il existe une version EXCEL5 et une version EXCEL97.
TELECHARGER : RADIO.ZIP (72 ko : les 2 fichiers excel + ce texte)
Description de l’activité :
1) Activité sans l’outil informatique
Pré requis : Les élèves connaissent les 3 sortes de radioactivité, l’existence de noyaux instables et les lois de conservation de la charge électrique et du nombre de nucléons.
TP : Le TP commence par une série d’une centaine de comptages à l’aide du CRAB du nombre de désintégrations détectées au voisinage d’un échantillon radioactif, pendant un court intervalle de temps (1s par exemple). Le professeur manipule et annonce à chaque fois le résultat obtenu.
Les élèves tracent l’histogramme au fur et à mesure sur une feuille de papier. Très vite ils voient apparaître une courbe en cloche.
2) Activité avec l’outil informatique
Idée : Utiliser la fonction ALEA() disponible sur un ordinateur pour tracer un histogramme d’un phénomène aléatoire. Par comparaison des deux histogrammes faire établir le lien entre le caractère aléatoire et la loi exponentielle de décroissance.
Les élèves disposent du tableau suivant qui représente l’état de 300 noyaux)(état initial)
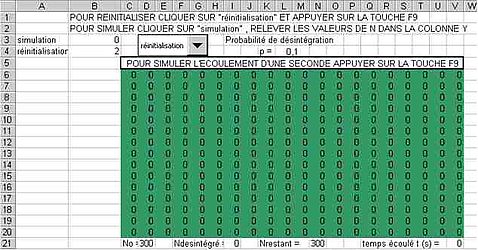
Chaque case verte de valeur 0 (chaque noyau) a une probabilité p de changer de couleur et de prendre la valeur 1 (de se désintégrer) dans la seconde qui suit (simulée par un appui sur la touche F9):
Par exemple, au bout de 8 pressions sur F9, le tableau peut prendre l’aspect suivant :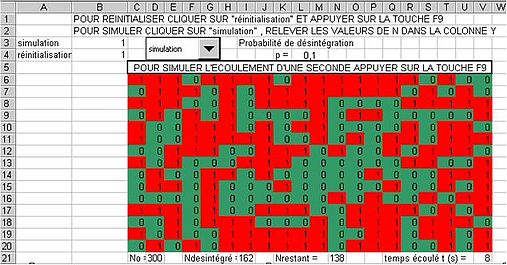
Exploitation des résultats :
- Les élèves font le relevé des valeurs du nombre de noyaux restants en fonction du temps. Ils peuvent remarquer que les séries de valeurs obtenues par leurs camarades ne sont pas rigoureusement identiques.
- Ils peuvent tracer la courbe N = f(t) manuellement, ou bien en utilisant Excel, ou un autre tableur, et confronter ce tracé avec le graphe d’une fonction N = N0.exp(-t)
(en utilisant la fonction courbe de tendance d’Excel).
- Ils peuvent en déduire la valeur de et la comparer à p.
- Ils peuvent chercher la valeur de la demi-vie T.
Consignes :
- L’utilisation de l’application est simple, il suffit de configurer Excel pour des références circulaires (« Outils Options Calcul Mode de calcul : Sur ordre ; Cocher la case Itération ; Mettre le nombre maximum d'itérations à 1 ») ;
- Quand le nombre de noyaux restants devient très petit (1 ou 2), et si on n’a pas de « chance » les dernières désintégrations peuvent prendre beaucoup de temps (un noyau ne vieillit pas !). Il n’est pas nécessaire d’atteindre N =300.
Bilan et perspectives :
- Contrainte matérielle : il faut disposer d’une salle informatisée.
- Temps de préparation : identique au temps de préparation de la séquence ne faisant pas intervenir l’outil informatique.
- Plus-value : Il existe des versions fastidieuses de ce TP effectué avec des dés que les élèves doivent lancer un grand nombre de fois. Avec l’outil informatique, le gain de temps est considérable et permet ici au professeur de consacrer plus de temps à l’étude de la loi de décroissance.
Complément : Il est possible de donner quelques précisions sur le fonctionnement du logiciel en détaillant le contenu d’une case du tableau, par exemple celui de la cellule C6 :
=SI(C6=0;SI(ALEA()<1-p;0;$B$3);$B$3)
