Présentation du projet
Synthèse : énoncés, analyses et travaux d'élèves .pdf .doc
Description rapide
- Au collège et 3ème prépa pro : Découverte de la notion d’équation avec la programmation par Scratch de tests au hasard, de tests par balayage puis de tests par balayage ciblé par l’utilisateur.
- En LGT : Reprise de la programmation par Python pour rechercher des solutions à des équations dont la méthode de résolution n’est pas connue en seconde. Approche de la méthode de dichotomie comme amélioration de la méthode par balayage.
- En LP : Utilisation d’un nouvel outil numérique (Scratch puis Python) pour formaliser une démarche de résolution du premier degré en seconde ; puis, en première, pour la résolution d’une équation du second degré. Utilisation d’une méthode par balayage (via scratch) pour faire une étude rapide lors de la résolution d’une problématique (recherche d’un extremum par exemple).
Niveaux concernés
- Au collège : quatrième et troisième
- En LGT : seconde
- En LP : 3ème prépa pro, seconde, première et Terminale
Logiciels Scratch et Python
Objectif général Aborder les équations avec l’algorithmique et la programmation en réinvestissant les compétences du cycle 4 en LGT et LP et en assurant une transition du logiciel Scratch vers Python.
Au collège
- TP informatique 1 « Programmer pour trouver des solutions »
Ce premier TP informatique propose aux élèves de créer des programmes sur Scratch qui permettent de trouver des solutions à différentes situations en procédant à différents tests. Le but est de montrer aux élèves, à la fin, que des programmes de simple test au hasard ne suffisent pas lorsque les recherches deviennent plus sophistiquées.
Créer un programme pour chaque situation donnée qui permette de trouver la ou les solutions attendues.
Situation 1
Antoine choisit un nombre. Il le multiplie par 3,5 puis il ajoute 7 au produit obtenu. Au final, il obtient – 35.
Quel nombre a-t-il choisi au départ ?
Situation 2
Pauline choisit un nombre. Elle le multiplie par – 6,8 puis elle soustrait 15 au produit obtenu. Au final, elle obtient – 33, 36.
Quel nombre a-t-elle choisi au départ ?
Situation 3
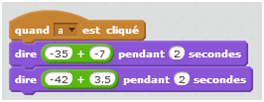
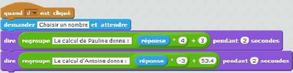
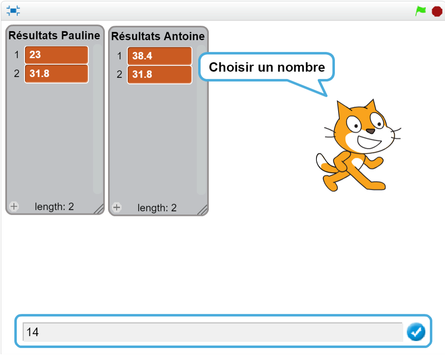
Pauline et Antoine choisissent tous les deux le même nombre au départ. Pauline multiplie ce nombre par 4 et ajoute 3 au résultat obtenu.
Antoine multiplie le nombre par – 3 et ajoute 53,4 au résultat obtenu.
Quand ils ont terminé, ils s’aperçoivent qu’ils obtiennent exactement le même résultat à la fin.
Quel nombre ont-ils choisi au départ ?
Améliorations possibles
Indiquer les avantages et les inconvénients de chacun des programmes réalisés et indiquer les améliorations possibles qui permettraient de créer des programmes plus performants pour répondre à ce genre de question.
Situation 4
| Programme de calcul A | Programme de calcul B |
| ∎ Choisir un nombre | ∎ Choisir un nombre |
| ∎ Multiplier par 7 | ∎ Multiplier par – 9 |
| ∎ Ajouter 15 | ∎ Ajouter 1 635,8 |
Pauline a choisi le même nombre au départ pour les deux programmes et a trouvé à la fin un même nombre.
Quel nombre a-t-elle choisi au départ ?
- TP informatique 2 « Découverte des listes »
Suite au premier TP informatique, il a été convenu que garder des scripts trop simples ne permet pas toujours de trouver facilement la solution recherchée. Ce TP informatique a pour but de faire découvrir l’utilisation des listes sur Scratch aux élèves. Ceux-ci pourront alors utiliser ces dernières pour trouver les solutions aux situations pour lesquelles ils ne trouvaient pas de solution auparavant. Par la suite, les élèves découvrent la recherche de solution par balayage. Celui-ci devient de plus en plus précis au cours du TP informatique. Tous les élèves ne peuvent pas atteindre la fin du TP. Ce TP doit être abordé par les élèves en fonction de leur compétence en programmation. L’objectif qui doit être atteint par tout le monde est l’acquisition de l’utilisation des listes. Les élèves ayant développé de plus grandes capacités en programmation peuvent aborder plus facilement la partie « balayage ». Ce TP informatique a pour but d’apporter aux élèves des connaissances supplémentaires pour répondre aux questions de recherche de solutions aux diverses situations et fournira aux élèves qui le souhaitent des outils déjà programmés et réutilisables pour le troisième TP informatique.
- Tester une expression pour les nombres entiers de 1 à 10
Créer un programme exécuté « quand a est cliqué ».
Le lutin donne la valeur de l’expression 2x + 7 quand x = 1 ; x = 2 ; x = 3 ; x = 4 ; x = 5 ; x = 6 ; x = 7 ;
x = 8 ; x = 9 et x = 10 et stocke ces valeurs dans une liste.
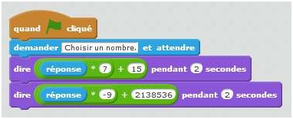
- Tester une expression pour dix nombres entiers consécutifs au choix
Créer un programme exécuté « quand b est cliqué ». Le lutin donne la valeur de l’expression 2x + 7 pour dix nombres entiers consécutifs choisis par l’utilisateur, et stocke ces valeurs dans une liste.
Aides
Pour comprendre le principe de la question réponse.
Pour comprendre le principe du stockage d’une donnée dans une variable.
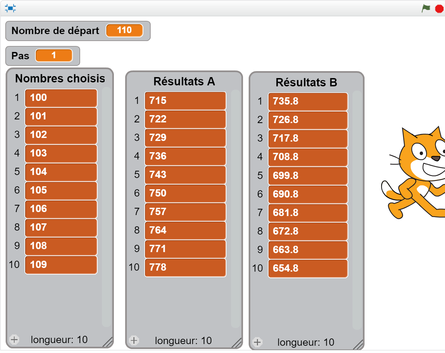
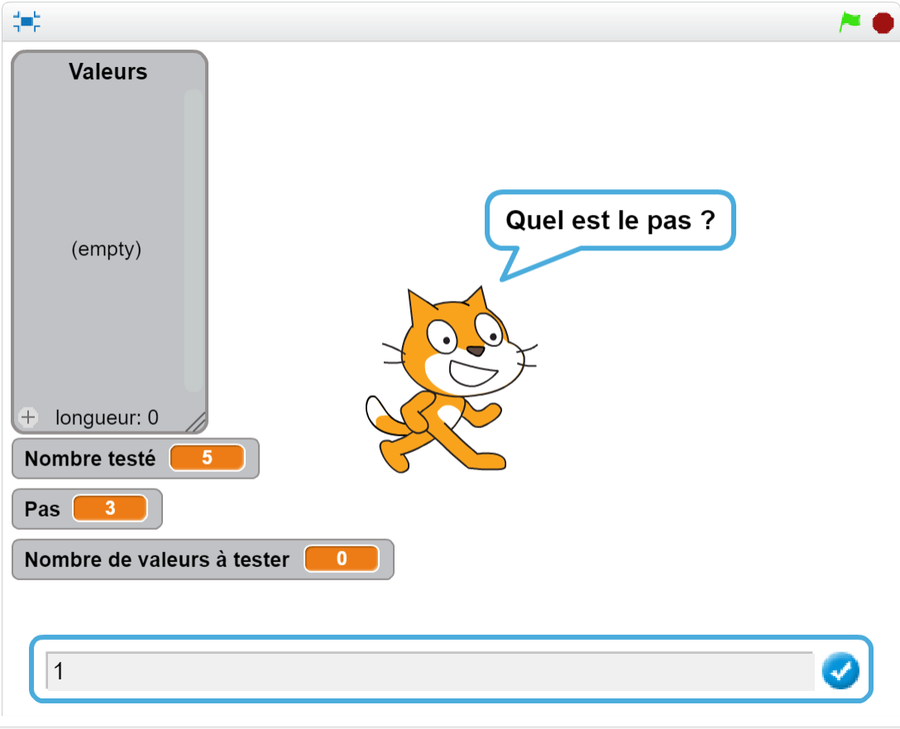
- Tester une expression pour dix nombres au choix
Créer un programme exécuté « quand c est cliqué ».
Le lutin donne la valeur de l’expression 2x + 7 pour dix nombres choisis par l’utilisateur.
L’utilisateur doit indiquer le premier nombre qu’il veut tester et le pas régulier entre les dix valeurs qu’il désire.
Les dix valeurs doivent être stockées dans une liste.
Exemples de pas :
1 ; 3 ; 5 ; 7 ; 9 ; 11 ; 13 le pas entre les valeurs est ici de 2.
9 ; 9,5 ; 10 ; 10,5 ; 11 ; 11,5 ; 12 le pas entre les valeurs est ici de 0,5.
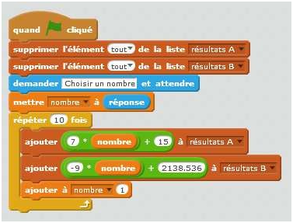
- Tester une expression pour plusieurs nombres au choix
Créer un programme exécuté « quand d est cliqué ». Le lutin donne la valeur de l’expression 2x + 7 pour plusieurs nombres choisis par l’utilisateur.
L’utilisateur doit indiquer le premier nombre qu’il veut tester et le pas régulier entre les valeurs qu’il désire et indique le nombre de valeurs qu’il veut tester.
Toutes les valeurs doivent être stockées dans une liste.
- TP informatique 3 « Utilisation des scripts précédents »
Ce troisième TP informatique propose aux élèves de trouver la solution à une situation similaire aux situations du premier TP informatique, mais la solution recherchée est plus difficile à trouver. Les élèves sont alors contraints de programmer des scripts plus sophistiqués s’ils veulent trouver la solution.
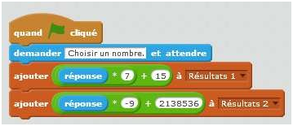
Situation 1
| Programme de calcul A | Programme de calcul B |
| ∎ Choisir un nombre | ∎ Choisir un nombre |
| ∎ Multiplier par 7 | ∎ Multiplier par – 9 |
| ∎ Ajouter 15 | ∎ Ajouter 2 138,536 |
Pauline a choisi le même nombre au départ pour les deux programmes et a trouvé à la fin un même nombre. Quel nombre a-t-elle choisi au départ ?
Situation 2
Considérons l’expression littérale A = x² + x − 2.
Pour quelle(s) valeur(s) de x, cette expression est-elle égale à 4 ?
- Activité « L’aquarium de Bubulle et Didier »
Cette activité est donnée après que les élèves ont vu en classe comment mettre un problème en équation et comment rechercher une solution à cette dernière à l’aide d’une calculatrice, du tableur ou du logiciel Scratch. Cette activité constitue donc un travail de fin d’apprentissage de la notion d’équation et de sa modélisation.
Les élèves ont la possibilité d’utiliser toutes les ressources dont ils disposent. Ils peuvent par conséquent utiliser le cahier d’exercices dans lequel des exercices avec Scratch ont été travaillés. Il leur suffit alors de recopier des modèles de scripts. De plus, ils peuvent réutiliser tous les travaux sur Scratch qui ont été réalisés avec eux au préalable
Énoncé
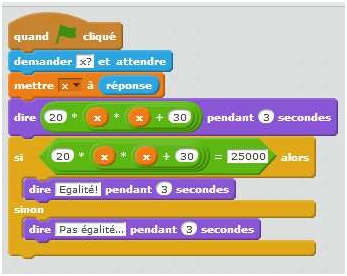
Bubulle et Didier ont grandi. Ils se sentent maintenant à l’étroit dans leur aquarium en pavé droit de 15L. Aïcha l’a compris et souhaite leur en construire un nouveau d’une capacité de 25L (soit 25 000 cm3). Comme ses étagères sont étroites, la base de l’aquarium doit être un rectangle de 20 cm de large. Aïcha voudrait aussi qu’il fasse 30 cm de plus en longueur qu’en hauteur.
Quelle doit être la hauteur de l’aquarium ?
- Mettre en équation cet énoncé.
- Modéliser ce problème à l’aide du logiciel Scratch pour trouver la réponse.
Au lycée d'enseignement général et technologique
- TP informatique 1 « Résoudre une équation avec Python »
Les élèves ont travaillé sur le problème "l'aquarium" proposé en collège, uniquement sur la partie mise en équation. Le TP propose de chercher une valeur approchée de la solution de l'équation avec un programme écrit en python.
Résoudre une équation avec Python
Objectif : Trouver une solution x0 de l’équation 20x² + 600x = 25 000 pour résoudre le problème de l’aquarium.
Partie 1
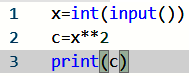
Dans l’éditeur, reproduire le programme ci-contre. L’exécuter plusieurs fois en changeant la valeur de départ de x et dire ce qu’il fait.
Avec une fonction.
Créer une fonction nommée c dont l’argument est un nombre x et qui renvoie le carré de x.
Tester cette fonction dans la console.
Créer une fonction nommée V dont l’argument est un nombre x et qui renvoie le volume de l’aquarium en fonction de x.
En faisant plusieurs tests, donner deux nombres entiers encadrant la solution xO cherchée.
Soyons plus précis, donner une valeur approchée de xO à 10–1 près.
Partie 2. Balayages.
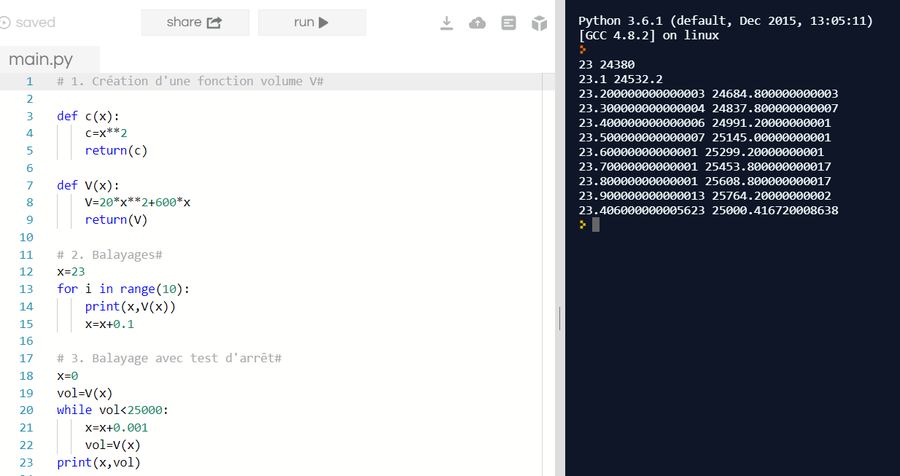
À la suite de ce qui a été fait dans la partie 1, reproduire le programme ci-contre. L’exécuter et dire ce qu’il fait.
On parle de « balayage » : pour la variable x, la valeur de début est …… et le pas est ……
En utilisant un autre balayage avec la fonction V, vérifier les résultats obtenus en partie1.
Partie 3. Des balayages qui s’arrêtent.
À la suite de ce qui a été fait dans la partie 1, reproduire le programme ci-contre. L’exécuter et dire ce qu’il fait.
En s’inspirant de la question a), donner une valeur approchée de x0 à 10–3 près.
Définir une fonction avec pour arguments :
- la valeur de départ de x : d.
- le pas : p
et qui renvoie :
- une valeur approchée de x0
- le volume correspondant à cette valeur approchée.
- Jeux informatiques « Un monstre et un chat » et « Devine un nombre »
- Attraper le monstre et recommencer jusqu’à obtenir le score maximal (40/40)
- Deviner un nombre.
| Ouvrir le fichier nombre entre 1 et 100. Cliquer sur le drapeau vert pour jouer avec le chat en proposant des nombres entiers. Faire 3 parties en trouvant le nombre secret avec un nombre minimum de tentatives. | Ouvrir le fichier nombre entre 1 et 1000. Faire 2 parties (avec un nombre minimum de tentatives) en remplissant des tableaux dont il faut remplir chaque ligne avec à chaque étape : • le nombre testé ; • + si le chat dit « plus grand », − sinon ; • l’intervalle (le plus petit possible) dans lequel se trouve le nombre à deviner. |
- TP informatique 2 « Un premier algorithme de dichotomie »
Résolution approchée de V(x) = 25 000 (à 10–4 près)
On veut déterminer une valeur approchée de la solution cherchée x0 par un procédé plus ingénieux que le balayage :
V(0) = 0 et comme V(50) = 20 × 50 × 80 = 80 000,
On peut en déduire que x0 est compris entre 0 et 50.
Information peu précise ! x0 appartient à [0 ; 50], intervalle d’amplitude 50.
Etape 1.
Alors on coupe [0 ; 50] en deux intervalles de même amplitude : [0 ; 25] et [25 ; 50]. Puis on détermine de quel « côté » se trouve x0 en calculant V(25).
Comme V est croissante sur [0 ; 50], on peut comparer x0 à 25.
Information plus précise : x0 appartient à un intervalle d’amplitude 25.
Etape 2.
Alors on coupe cet intervalle en deux intervalles de même amplitude.
Et ainsi de suite. On peut ainsi compléter le tableau ci-dessous :
| Intervalle [a ; b] | Amplitude | Centre n de [a ; b] | V(n) ≃… | Donc n prend le rôle de… | |
| Etape 1 | [0 ; 50] | 50 | 25 | ||
| Etape 2 | |||||
| Etape 3 |
Fastidieux ! À Python d’exécuter cet algorithme pour nous, en créant une fonction nommée « dicho » :
• l’argument p de dicho correspondra à la précision souhaitée (c’est-à-dire que l’amplitude du dernier intervalle [a ; b] doit être plus petite que p)
• dicho doit renvoyer la dernière valeur de n.
Au lycée professionnel
- Activité « L’emballage »
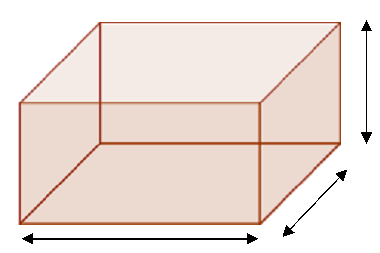
Une usine d’emballage reçoit la commande d’une entreprise pour la conception d’un contenant de 25 L, soit 25 000 cm3, avec les contraintes suivantes : une profondeur de 20 cm, une hauteur non définie mais une largeur de 30 cm de plus que la hauteur.
Quelle doit-être la hauteur de l’emballage afin d’obtenir un volume de 25 000 cm3 ?
1. À l’aide d’une inconnue, inscrire les côtes sur le schéma ci-contre.
2. Vérifier que le volume de la boite, pour une hauteur de 10 cm, est de 8 000 cm3.
3. Exprimer le volume de la boite en fonction de x.
4. Proposer une méthode, permettant de déterminer la hauteur nécessaire.
Appel professeur : proposer votre protocole afin de le réaliser.
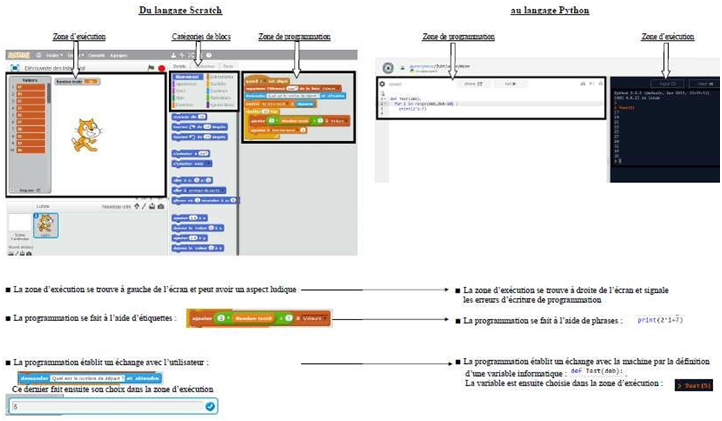
Bilan : passage du logiciel Scratch au logiciel Python
Passage de Scratch à Python au collège :
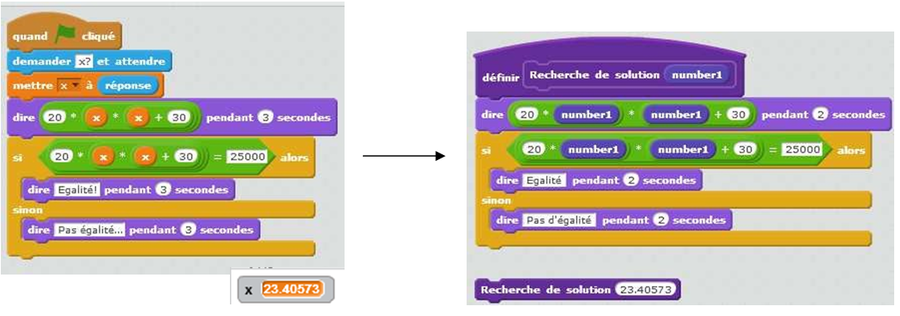
Pour habituer les élèves avec Scratch à ne plus s’adresser à un utilisateur mais à l’ordinateur, comme ils devront le faire avec Python, il est possible d’inciter ces derniers à ne plus utiliser l’étiquette « demander » et à préférer la création d’un bloc avec une entrée. Ils s’habituent ainsi à la création d’une fonction avec une variable.
Passage de Scratch à Python au lycée :
Une difficulté que rencontrent les élèves avec le logiciel Scratch est la programmation d’une succession de calculs. Multiplier l’emboîtement d’étiquettes les unes dans les autres peut rapidement devenir difficile. Ce problème n’est pas rencontré avec Python. Ce constat peut servir de point d’appui pour justifier l’utilisation d’un nouveau logiciel de programmation en classe de seconde.