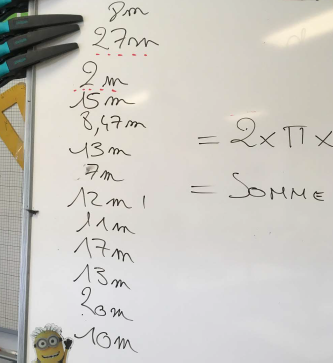| Tâches | Niveau | Numérique | Domaine mathématique | Description | Durée |
|---|---|---|---|---|---|
| T1 T3 | Cycle 4, Lycée | Tableur Scratch | Géométrie Algorithmique | Les élèves doivent estimer la longueur d’une corde enroulée sur elle-même | 15mn – 30 mn |
Énoncé
Estimer la longueur de la corde.
Données :
Diamètre de la corde : 10mm.
Diamètre spirale : 26cm.

Descriptif
Proposition de scénario d'usage :
On laisse d'abord les élèves essayer d'estimer la longueur d'une corde enroulée en spirale. Puis, trois modèles sont ensuite proposés. On compare les différentes réponses.
Intentions du concepteur :
- Interroger le modèle au regard de la situation (pertinence des résultats obtenus, cohérence, domaine de validité...). Exemple : Comparer 2 modèles au regard des enjeux liés à la situation réelle.
- Expliciter les choix et les renoncements effectués lors d'une modélisation.
Place dans la progression, moment de l'étude :
- Après avoir vu le périmètre d'un cercle.
- Après avoir travaillé sur les variables dans un algorithme.
- Après avoir travaillé différentes formules dans le tableur (=SOMME ...)
Rapport d'expérimentation
En estimant « à l’oeil » voici ci-contre les réponses des élèves.
Le débat sur les valeurs extrêmes (2m et 27 m) est ouvert : en faisant estimer rapidement la taille du collège à 15m, l’élève qui a proposé cette réponse (27m) change
rapidement d'avis et propose 10m.
Deux modèles sont proposés par les élèves. Pour le premier, l’élève demande le nombre de tours (il y en a 13) puis en conclu immédiatement que la corde fait 13m... Pour le deuxième modèle, un autre élève demande le rayon de la spirale afin de calculer ce qu'il appelle le « tour extérieur», sa démarche s’arrête là ...
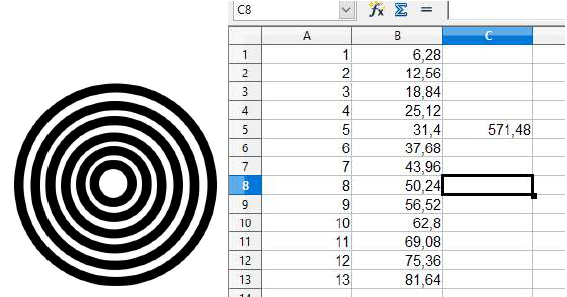
Le premier modèle avec utilisation du tableur est projeté. Les élèves semblent comprendre le procédé, les formules entrées dans le tableur sont données rapidement par plusieurs élèves, l'estimation leur paraît correcte.
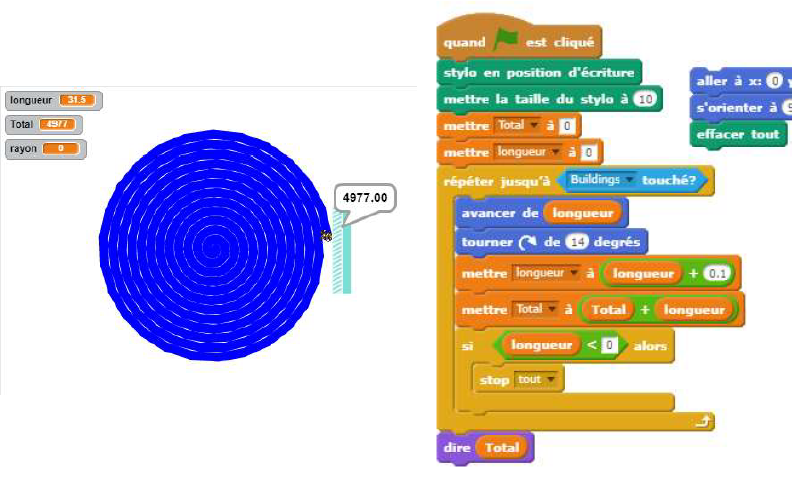
Le deuxième modèle avec utilisation de scratch est projeté. Les élèves donnent très rapidement du sens à l’algorithme, sa compréhension ne semble pas poser de problèmes même si l'explication de l'angle de 14° est floue... Ils donnent sans difficulté les coordonnées du « mur ». Il y a une discussion sur l'unité du 4995. Une élève qualifie ce modèle de « sympathique ».
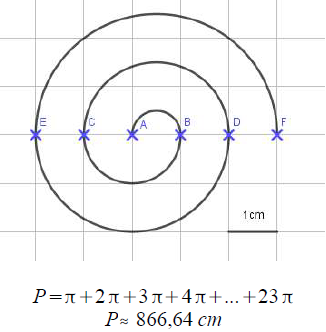
Le troisième modèle est projeté. Ce modèle ne convainc pas les élèves. Ils ne sont pas capables de verbaliser pourquoi.
La corde mesure en réalité 5m . Une discussion s'ouvre sur la validité des modèles. Un élève trouve que le dernier modèle est « nul », il trouve qu'une différence de 3m par rapport à la réalité est trop importante. Une discussion est ouverte, une erreur de 3m pour le calcul de la circonférence de la terre est–ce aussi une grosse erreur? Cela débouchera sur le calcul d'un pourcentage d'erreur.
Fichiers
 corde_m1.ggbQuatrième modèle
corde_m1.ggbQuatrième modèle corde_m2.ggbCinquième modèle
corde_m2.ggbCinquième modèle spirale_2.sb2Sixième modèle
spirale_2.sb2Sixième modèle