| Tâches | Niveau | Numérique | Domaine mathématique | Description | Durée |
|---|---|---|---|---|---|
| T2 T3 | Troisième Seconde | Non | Géométrie | Choix d’un modèle géométrique permettant de modéliser la distance à l’horizon à partir d’une photo | 20 mn |
Énoncé
À quelle distance est l’horizon ?
Pour calculer la distance séparant la ligne d’horizon d’une personne située sur une plage il faut une modélisation et des données numériques permettant d’exploiter cette modélisation.
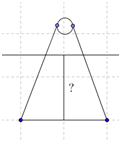
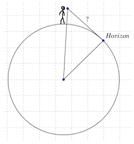
Parmi les modélisations suivantes de la situation, laquelle (ou lesquelles) peut (ou peuvent) permettre de répondre à la question posée après avoir cherché ou approximé les données numériques manquantes ? Si vous estimez qu’aucune ne peut permettre de répondre, vous pouvez élaborer votre propre modélisation dans le cadre dédié.




Images sous licence CC0 (obtenues via Pixabay et Pixnio)
Descriptif
Proposition de scénario d'usage :
La fiche élève est distribuée : les élèves doivent argumenter leur réponse. On effectue alors une synthèse collective.
En prolongement on peut demander un calcul effectif de la distance de l’horizon.
Intentions du concepteur :
- Travailler deux tâches de modélisation dans un temps relativement court.
- Mobiliser un cadre mathématique permettant de modéliser.
- Expliciter les choix et les renoncements effectués lors d’une modélisation.
Place dans la progression, moment de l'étude :
Indifférent.
Retour d'expérience :
Les modélisations 2 et 3 sont plébiscitées par une majorité d’élèves. Les justifications sont souvent concises mais permettent une mutualisation intéressante.
On peut faire remarquer aux élèves qu’à condition d’avoir des outils de mesure d’angle ou de hauteur très précis les modélisations 3 et 4 peuvent permettre de répondre à la question.
Fichier
 horizon.pdfFiche élève
horizon.pdfFiche élève