| Tâches | Niveau | Numérique | Domaine mathématique | Description | Durée |
|---|---|---|---|---|---|
| T1 T2 T3 | Cycle 4 | Non | Volume d’un solide et proportionnalité | Les élèves doivent estimer une masse de beurre. | 30 mn |
Énoncé

Estimer la masse de beurre.
Données


Réponse
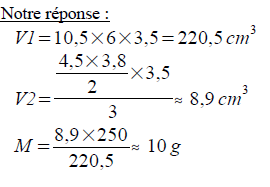

A -t-on commis une « erreur » ? Notre réponse est-elle acceptable ? Peut-on mieux faire ?
Descriptif
Proposition de scénario d'usage :
Les élèves essayent d'estimer la masse beurre et exposent leur démarche avant de se lancer dans les calculs.
Intentions du concepteur :
- Travailler la modélisation.
- Interroger le modèle au regard de la situation (pertinence des résultats obtenus, cohérence, domaine de validité...)
- Mobiliser un cadre mathématique permettant de modéliser.
- Expliciter les choix et les renoncements effectués lors d'une modélisation.
Place dans la progression, moment de l'étude :
Après avoir vu le volume de la pyramide et du pavé droit.
Rapport d'expérimentation
A partir d'un exercice classique du type :
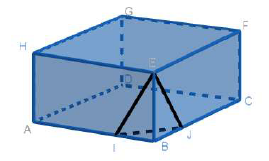
On considère le parallélépipède rectangle ABCDEFGH.
I est un point de [AB] et J est une point de [BC].
AB=8cm , BE= 3cm, BC= 7cm, IB=BJ=2cm.
Trouver le volume de la pyramide de sommet E et de base BJI.
On peut transformer rapidement l’énoncé pour mettre en valeur la modélisation.

En estimant « à l’oeil » voici, ci-dessus, les réponses des élèves.
Le débat sur les valeurs extrêmes (10g et 500g) est ouvert. L’élève qui a proposé 500g change rapidement d'avis.
Un premier élève propose de faire « pour 1 » mais est incapable d'expliquer ses intentions. Un autre rebondit sur cette remarque et demande à combien 1cm3
correspond en grammes.
Un autre élève intervient et dit qu'il faudrait connaître le « triangle ». Ce terme est immédiatement rectifié par un camarade. Une autre élève demande : « mais est-ce qu'on considère que la pyramide est parfaite ? »
L’élève qui avait parlé de triangle reprend la parole et demande si on peut calculer l'aire de la pyramide... Le professeur répète cette phrase plusieurs fois avant qu'un élève rectifie la phrase et parle de volume.
Une élève propose d'utiliser Thalès, un exercice dans un pavé sur ce thème avait été traité 2 jours auparavant... Elle n'ira pas plus loin dans sa proposition.
Un élève demande de : « convertir le volume en masse ».
Un autre élève demande si il s'agit bien de proportionnalité. Un élève propose de calculer, quel pourcentage représente la pyramide par rapport au pavé, il formule parfaitement son procédé, l'appliquera et trouvera lui aussi une réponse cohérente .
Les données sont projetées, une élève demande comment ont été trouvées les dimensions de la plaquette de beurre, a- t-on mesuré ?
Le calcul du volume du pavé ne pose pas de problème. En revanche, le calcul du volume de la pyramide est problématique (erreur formule aire du triangle par ex…) Peu d’élèves enchaînent ensuite avec la proportionnalité.
La photo de la pyramide de beurre sur la balance est projetée, les élèves sont très embêtés de ne pas avoir trouvé la réponse, un bon nombre pense avoir fait une erreur de calcul …
A contrario, un élève lui pense que c'est la balance qui n'est pas précise puis il dit que nous avons pris des arrondis et que donc notre réponse est une valeur approchée. Il est alors rappelé aux élèves que les dimensions ont été mesurées …
Une définition de la pyramide leur est donnée, une élève revient sur le fait qu'il ne s'agit pas exactement d'une pyramide.